Ecuaciones de (MRUA)

Las ecuaciones del movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) son:

v=v0+a⋅t
x=x0+v0t+12at2
a=cte

Donde:
x, x0: La posición del cuerpo en un instante dado (x) y en el instante inicial (x0). Su unidad en el Sistema Internacional (S.I.) es el metro (m)
v,v0: La velocidad del cuerpo en un instante dado (v) y en el instante inicial (v0). Su unidad en el Sistema Internacional es el metro por segundo (m/s)
a: La aceleración del cuerpo. Permanece constante y con un valor distinto de 0. Su unidad en el Sistema Internacional es el metro por segundo al cuadrado (m/s2)
t: El intervalo de tiempo estudiado. Su unidad en el Sistema Internacional es el segundo (s) 
Aunque las anteriores son las ecuaciones principales del m.r.u.a. y las únicas necesarias para resolver los ejercicios, en ocasiones resulta útil contar con la siguiente expresión:


v2=v20+2⋅a⋅∆x

La fórmula anterior permite relacionar la velocidad y el espacio recorrido conocida la aceleración y puede ser deducida de las anteriores, tal y como puede verse a continuación.


{v=v0+a⋅tx=x0+v0⋅t+12⋅a⋅t2⇒{t=v−v0a∆x=v0⋅t+12⋅a⋅t2⇒∆x=v0(v−v0a)+12⋅a⋅(v−v0a)2;


2⋅a⋅∆x=v2−v20
Deducción ecuaciones m.r.u.a.

Para deducir las ecuaciones del movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) hay que tener en cuenta que:
La aceleración normal vale cero: an=0
La aceleración media, la aceleración instantánea y la aceleración tangencial tienen el mismo valor: a=am=at=cte

Con esas restricciones nos queda:


am=aam=ΔvΔt=v−v0t−t0=t0=0x−x0t⎫⎭⎬⎪⎪→v−v0=a⋅t→v=v0+a⋅t

Esta primera ecuación relaciona la velocidad del cuerpo con su aceleración en cualquier instante de tiempo y se trata de una recta (v) cuya pendiente coincide con la aceleración y cuya coordenada y en el origen es la velocidad inicial (v0). Nos faltaría por obtener una ecuación que nos permita obtener la posición. Para deducirla hay distintos métodos. Nosotros usaremos el teorema de la velocidad media o teorema de Merton:
"Un cuerpo en movimiento uniformemente acelerado recorre, en un determinado intervalo de tiempo, el mismo espacio que sería recorrido por un cuerpo que se desplazara con velocidad constante e igual a la velocidad media que el primero"
Esto implica que:
 
∆x=vm⋅t

El valor de la velocidad media, en el caso de que la aceleración sea constante, se puede observar claramente a partir de la siguiente figura:






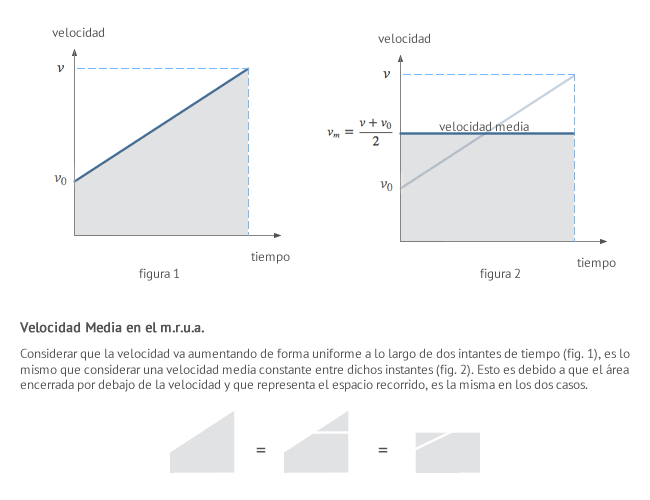
vm=v+v02

Si desarrollamos las ecuaciones vistas hasta ahora obtenemos la ecuación de la posición en el movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.):


∆x=x−x0=vm⋅t=1v+v02t=2v0+at+v02t=2v0+at2t=22v0t+at22⇒x=x0+v0t+12at2

Donde hemos aplicado:

vm=v+v02
v=v0+a⋅t

Por último, indicarte que en las ecuaciones anteriores se ha considerado que el movimiento se realiza en el eje x. Si nos moviéramos en el eje y, por ejemplo en los movimientos de caida libre o de lanzamiento vertical, simplemente sustituirías la x por la y en la ecuación de posición, quedando:
y=y0+v0t+12at2